Zurück zum Inhaltsverzeichnis   

Ausflug in die Welt der Zahlen

Ein wildes Essay ohne wissenschaftlichen Anspruch

«Wieviele Werke des gleichen Stils sollte man haben, damit man diese als Serie präsentieren kann?»

Mit dieser Frage beginnt meine Gedankenreise durch die Welt der Zahlen. Wenn ich von Gegenständen rede, egal ob es Äpfel, Birnen, Gemälde oder Fotos sind, ist es klar, dass wir uns in der Welt der natürlichen Zahlen bewegen. Das sind die ganzen Zahlen über Null, ohne Kommastellen. (Null und negative Zahlen stellen sozusagen die nummerische Unterwelt dar.) So wurde das jedenfalls von der Mathematikergemeinde festgelegt.

Zurück zu meiner eingangs gestellten Frage, wieviele Exemplare für eine Serie wünschenswert sind. Spontan denke ich an zehn. Das scheint mir eine respektable Zahl. Allerdings, wenn es um Kunst geht, erscheint die Zehn sehr nüchtern, technisch – die Repräsentation des Dezimalsystems. Da wäre vielleicht die Zahl zwölf – ein Dutzend – organischer, vielleicht gar magischer. Tatsächlich wird die Zahl Zwölf schon seit Jahrhunderten als magische Zahl angesehen. Man trifft sie auch auf den Märkten und bei alten Währungssystemen an. Obwohl wir in nach–napoleonischer Zeit fast gänzlich mit dem Dezimalystem operieren, kaufen wir z.B. die Eier immer noch im Dutzend oder Halbdutzend. Auch das Sixpack in dem Bier und Softdrinks angeboten werden, weist in diese Richtung. Die Amerikaner halten immer noch am alten Masssystemen fest, in dem 12 inch (Zoll) 1 Foot (Fuss) sind.

Die Zehn

Auf den ersten Blick konstatiere ich, dass schon die alten Römer mit dem Dezimalsystem operierten. Das erschliesst sich aus der Schreibweise der römischen Zahlen: X = 10. Das Dezimalsystem eignet sich gut zum Rechnen. Wir können dazu die zwei mal fünf Finger unserer Hände zu Hilfe nehmen. Interessanterweise geht das biologische Prinzip der fünf Finger (auch der Zehen) Millionen von Jahre zurück in der Evolution und gilt für alle Säugetiere. (Was die Säugetiere auch gemeinsam haben sind sieben Halswirbel – aber das ist eine andere Geschichte.) Man kann also ruhig behaupten, dass das Dezimalsystem tief in unserem Genom verwurzelt ist, auch wenn wir es generell als modern und technisch wahrnehmen. Mit den Computern hat  das Rechnen im Binärsystem die Welt erobert. Die Rechenvorgänge werden permanent vom Dezimalsystem ins Binärsystem (0/1 – Off/On) übersetzt und umgekehrt.

Wenn die Zehn so viele praktische Vorzüge hat, warum hat das Dutzend (das auch Teil des Dezimalsystems ist) eine so grosse Verbreitung gefunden?

Das Dutzend

Warum erscheint mir die Zwölf organischer als die Zehn? Faktisch trifft das ja gar nicht zu. Organischer, biologischer kann eine Zahl gar nicht sein, als eine, der unsere zehn Finger zugrunde liegen und die Millionen von Jahren in der Evolution verwurzelt ist. So gesehen ist die Beliebtheit der Zwölf eher kulturell begründet. (Vielleicht könnte man sagen: symbolträchtig, mystisch.) 

Es gibt viele Referenzen zur Zwölf. 

Der Tag ist in 2 mal 12 Stunden eingeteilt.

Die Stunden, wie die Wochentage sind willkürlich festgelegt (kein astronomischer Bezug).

Alte Währungs- und Masssysteme sind in Zwölf unterteilt.

Mittelalterliche Währungen, die bis auf die Römer zurückgehen: 
12 pence = 1 shilling, 20 shilling = 1 pound 

Bis 1973, als der Shilling abgeschafft wurde und das Pfund neu 100 Pence enthielt. 

Typografisches Masssystem: 12 Punkt = 1 Cicero
Ist immer noch aktuell bei der Schriftgrösse.

Amerikanisches Masssystem: 12 inch (Zoll) = 1 Foot (Fuss).

In Europa wurde dieses Masssystem Ende des 19. Jh durch das Dezimalsystem ersetzt (mm–cm–m).

Dann gibt es die 12 Apostel, 12 Monate¹, 12 Sternzeichen usw.

¹Die Monatsbezeichnungen September (7), Oktober (8), November (9), Dezemeber (10) kommen daher, weil im ursprünglichen römischen Kalender das Jahr mit dem März begann. In einer Agrargesellschaft beginnt das Jahr mit dem Frühling. Nach dem dunklen, kargen Winter beginnt neues Leben zu spriessen.

Vergleich zwischen Zehn und Dutzend

Mir fällt auf, dass die Zwölf mehr Teiler hat, als die Zehn. Die Zehn enthält 2 Teiler (2 und 5). Das Dutzend deren 4 (2, 3, 4 und 6). So gesehen ist das Dutzend reichhaltiger als die Zehn. Interessanterweise sind die zwei nächstliegenden Zahlen zur Zwölf – 11 und 13 – Primzahlen. Also Zahlen ohne Teiler (ausser 1 und sich selbst). Die 5 und 2, die Teiler von Zehn sind auch Primzahlen.

Die in Zwölf enthaltenen Teiler bieten Verweise auf mythische und phylosophische Inhalte:

Das grundsätzlichste Prinzip intellektuellen Denkens ist die Dualität, das Denken in Gegensatzpaaren. Das Endliche ist einfach zu erkennen – als Gegensatz schliessen wir auf das Unendliche*, dass sich unserer Vorstellungskraft entzieht. Viele Entscheidungsprozesse beginnen mit ja oder nein. Im Yin-Yang-Symbol ist die Dualität dargestellt. Das Prinzip von These und Antithese, von denen jede einen Kern ihres Gegenteils in sich trägt.

* Es gibt unendlich viele natürliche Zahlen. Und zwischen zwei natürlichen Zahlen gibt es unendlich viele Brüche. Dann müsste es ja unendlich mehr Zahlen mit Kommastellen geben, als natürlichen Zahlen. Das würde heissen dass die Zahl der Brüche unendlicher ist als die Zahl der natürlichen Zahlen …

Yin Yang

Aus These und Antithese lässt sich die Synthese ableiten. Das bringt uns zur Zahl 3. Für die Drei gibt es etliche mythische Referenzen. Z.B. „Vater, Sohn und heiliger Geist“ (die heilige Dreifaltigkeit). Oder Buddha, Dharma und Samgha im Buddhistischen Glauben (Trinatna).

Die Verdoppelung von 2 und 3 ergibt 4 und 6. Darauf ist z.B. das I Ging (chinesisches Orakel) aufgebaut. 1 (ungerade) ergibt eine durchgehende Linie, 2 (gerade) ergibt eine unterbrochene Linie. Ein fertiges Symbol besteht aus 2 Gruppen von 3 übereinander liegenden Linien (= 6 Linien). Es gibt 64 Symbole.

Primzahlen

Das sind die Zahlen, die keine Teiler enthalten (ausser sich selbst und eins – was unvermeidlich ist). Ausser 2 sind alle Primzahlen ungerade. Die 1, obwohl der Definition einer Primzahl entsprechend, wird von der Mathematiker-Gemeinde nicht als Primzahl angesehen. Das gibt der Zahl 1 eine Sonderstellung. Sie repräsentiert das Ganze. Die Primzahlen mischen sich in loser, unregelmässiger Folge in die  Zahlenreihe. Bernhard Riemann hat Mitte des 19. Jahrhunderts eine Formel aufgestellt, aufgrund derer ein Zusammenhang zwischen den Primzahlen vermutet werden kann. Dieses Phänomen ist bekannt unter dem Begriff „Riemannsche Vermutung“². Es haben seither viele Mathematiker versucht, das Geheimnis der Riemannschen Vermutung zu entschlüsseln, was bisher aber keinem gelungen ist. Deshalb gilt die Riemannsche Vermutung als eines der grossen ungelösten Rätsel der Mathematik. Ich hätte eigentlich erwartet, dass bei sehr grossen Zahlen irgendwann keine Primzahlen mehr erscheinen. Aber es wird berichtet, dass sich die Primzahlen bis ins Unendliche fortsetzen. Ohne erkennbares Muster in ihrem Erscheinungsrhythmus. Ihrer Natur nach enthalten Primzahlen keine „Bruchstellen“ (Teiler). Deshalb kann man sie als hart und stabil ansehen. Zahlen mit vielen Teilern erscheinen dann eher als weich, mit vielen „Bruchstellen“.

²Riemannsche Vermutung: «Alle möglichen nichttrivialen Nullstellen befinden sich auf dem sogenannten „kritischen Streifen“».

Zahlensysteme

Das wichtigste ist natürlich das Dezimalsystem, in dem auch das Dutzend enthalten ist. Auch einen wichtigen Platz nimmt in der modernen Welt das Binärsystem ein. Denn die ganzen Rechenfunktionen der Computer basieren auf diesem System. Die Rechenvorgänge werden permanent vom Dezimalsystem ins Binärsystem übersetzt und umgekehrt.

Es besteht aus 2 „Grundziffern“: 0 (Off) und 1 (On), die man Bit nennt. 

Beispiel: Im Binärsystem entspricht die 10 der Zahl 2 im Dezimalsystem

Im Computer wird das Binärsystem auf der Grundlage von 4 Bit dargestellt. Ein solche Gruppe nennt man Bite

Vergleich Binär- / Dezimalsystem:

Die Verwendung von 4er Gruppen verweist auch wieder auf die Zahl 4 als Teiler von 12. Um die Schnelligkeit zu erhöhen, können Computer ganze Pakete von Bits auf einmal lesen. Diese Pakete basieren generell auf dem Faktor 4. Moderne Rechner verwenden 16- oder 32-Bit Technologie, d.h. sie können Ketten von 16 oder 32 Bit auf einen Blick „lesen“.

Interessanterweise ist die Speicherkapazität von Smartphones und Tablets so ausgelegt, dass darin der Faktor 4 enthalten ist. Z.B. 32 GB,

64 GB, 128 GB etc.

Analog zum Binärsystem sprechen wir auch vom Dualsystem, das Denken in Gegensatzpaaren (richtig-falsch, ein-aus endlich-unendlich etc.). Auch das Morsen basiert auf einem Binärsystem (kurz-lang).

Es ist möglich, in allen beliebigen Zahlensystemen zu rechnen. Z.B. im 6er-System. Dort wird die Zahl 6 als 10 ausgedrückt:

01 – 02 – 03 – 04 – 05 – 10

11 – 12 – 13 – 14 – 15 – 20

Jedenfalls müsste es so funktionieren, wenn man die selben Grundsätze anwendet, wie beim Dezimalsystem. (Die Recherche auf dem Netz bestätigt meine Vermutung.) Wenn ich jedoch das Dezimalsystem näher betrachte, mache ich eine überraschende Entdeckung – etwas, das mir bis anhin noch nicht aufgefallen war: Das Dezimalsystem bedient sich der Grundziffern 1 bis 9. Die 10 ist also der Beginn der zweistelligen Zahlen und gleichzeitig das Ende der ersten Zehnergruppe. Während in einem 6er System hinter der 10 die 6 verborgen ist, ist im Dezimalsystem die 10 die Zehn. D.h. die 10 ist sozusagen die Null der nächstfolgenden 2-stelligen Zehnergruppe. Wenn man die Null  in die Schreibweise einbeziehen würde, sähe das folgendermassen aus:

00 – 01 – 02 – 03 – 04 – 05 – 06 – 07 – 08 – 09

10 – 11 – 12 – 13 – 14 – 15 – 16 – 17 – 18 – 19 …

obwohl diese Schreibweise logisch wäre ist sie für uns verwirrend. Wir sind es uns so gewohnt:

01 – 02 – 03 – 04 – 05 – 06 – 07 – 08 – 09 – 10

11 – 12 – 13 – 14 – 15 – 16 – 17 – 18 – 19 – 20

·

·

·

91 – 92 – 93 – 94 – 95 – 96 – 97 – 98 – 99 – 100 etc.

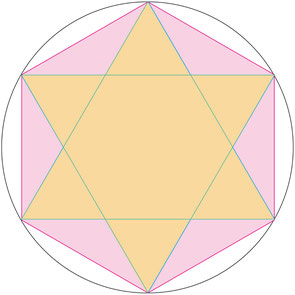
Das Hexagramm

Die Zahl 6 kommt auch in vielen mythischen Zusammenhängen vor.

666 als Symbol für den Teufel. (Interessanterweise hat jedoch der Satansstern 5 Zacken.)

Wenn man einen Kreis zeichnet und dann per Zirkel den Radius auf dem Umfang abträgt, erhält man 6 gleich grosse Segmente. Daraus entsteht ein Hexagramm, wenn man die abgetragenen Punkte mit Strecken verbindet (deren Länge entspricht dem Radius). Aus dieser Situation lässt sich auch der Davidstern ableiten.

Auch hier ein Bezug zur Zahl 12 (6 als Teiler von 12).

Die Oktave

Mit der Oktave hat es eine spezielle Bewandtnis. Die Oktave ist in der Musik der Abstand zwischen zwei Tönen, deren Frequenzen sich im Verältnis 1:2 verhalten. Also z.B. vom mittleren C zum Hohen C.

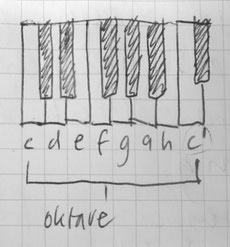
Die Töne werden mit Buchstaben bezeichnet, nicht mit Zahlen. Ich erinnere mich auch an meine Schulzeit,, als wir im Gesangsunterricht die Noten wie folgt lernten (ich weiss das heute, nach 50 Jahren, noch auswendig):

DO  RE   MI   FA   SO  LA   TI   DO

 c      d      e      f      g      a      h     c

Es existieren dafür auch Handzeichen, nach denen uns der Lehrer Töne singen liess:

Damit die Tonleiter harmonisch tönt, hat es (in der c-dur) zwischen e und f einen Halbtonschritt. Innerhalb der Oktave gibt es noch fünf Halbtöne zusätzlich, die mit den Ganztönen zusammen die chromatische Tonleiter bilden. Diese besteht aus 12 Tönen (das obere c nicht mitgerechnet). 

Die Zwöltonmusik bedient sich dieser Tonleiter als gleichwertige Töne. Das gibt der Zwölfton-Musik eine disharmonische Anmutung.

Ganz nebenbei: Da treffen wir schon wieder auf die Zahl 12. Die Gruppierung der schwarzen (Halbton-)Tasten – 2 und 3 – entsprechen Teilern von 12. (Alles Zufall oder was?)

Wenn man die Oktave in Zahlen ausdrückt, entspricht sie allerdings nicht dem Oktalsystem. Das obere c müsste der 11 entsprechen. Daraus ergibt sich folgende Schreibweise:

  c       d      e      f       g      a     h

01 – 02 – 03 – 04 – 05 – 06 – 10

 c’     d’     e’     f’     g’     a’    h’

11 – 12 – 13 – 14 – 15 – 16 – 20

Die Oktave entspricht also in der Zahlenwelt einem Septimalsystem (7).

Wenn wir schon bei der Musik sind können wir uns auch noch mit den Takten beschäftigen:

In der westlichen Hemisphäre ist der 4/4-Takt der Goldstandard. Rock, Pop, Jazz, Tanz- und Volksmusik, Kirchenlieder und Klassische Musik basiert im überwiegenden Mass auf dem 4/4-Takt. Eine Ausnahme bildet der Walzer, der im 3/4-Takt gespielt wird. Die Notenschrift basiert auf einem System, dessen rhythmische Grundlage ein Takt ist der einer ganzen Note entspricht. Die Noten können dann halbiert, geviertelt, geachtelt ode gesechzehntelt werden. Daraus ergibt sich, dass beim Walzer (1-2-3 – 1-2-3 …) ein Takt aus 3 Viertelnoten besteht. In der nahöstlichen Volksmusik begegnet man oft dem 6/8-Takt, bei dem dann ein Takt 6 Achtelnoten entspricht. Der 6/8-Takt unterscheidet sich vom 3/4-Takt insofern, als dass die Betonung auf den 6. Schlag folgt (1-2-3-4-5-6 – 1-2-3-4-5-6 …). Wir ahnen auch hier eine Beziehung zur 12 (3-4-6). Es scheint, dass unser natürliches Taktgefühl auf Teilern von 12 basiert. In der traditionellen orientalischen und asiatischen Musik, die nicht wirklich eine Notenschrift kennt, spielt die Intuition eine grosse Rolle und es wird auch in 5er, 7er und 9er-Takten gespielt. (Falls überhaupt ein metronomischer Unterbau vorhanden ist.) Gezählt wird natürlich in dieser Musik auch. So kann ein 9er Takt verschieden betont werden. Z.B. 1-2-3 – 1-2-3-4 – 1-2 usf. Im Jazz oder Progrock werden solch „schräge“ Takte manchmal implementiert. Ein bekanntes Beispiel ist „Take 5“ von Dave Brubeck (im 5/4-Takt). Bei Zappa und Genesis findet man auch Taktbilder, die nicht auf 4 aufgehen. Die Musiker müssen sich dann darauf konzentrieren, das vorgegebene Rhythmusmuster strikt einzuhalten. Heute wird auch orientalische Musik, um dem westlichen Ohr zu gefallen, durchaus im 4/4-Takt gespielt.

Die Sieben

7 Tage pro Woche: Während die Monate und die Jahre einen Bezug zur Himmelsmechanik haben, sind die Wochentage willkürlich festgelegt. Eigentlich hatte die Arbeitswoche der alten Semiten 6 Tage (so lange hat Gott gebraucht, um die Welt zu erschaffen). Der siebte Tag ist der wohlverdiente Ruhetag. In postindustrieller Zeit haben wir offiziell 5 Arbeitstage und 2 Ruhetage (ganz nebenbei die Teiler von 10).

Alle Säugetiere haben 7 Halswirbel (Wale und Giraffen einbezogen).

Die Schweiz hat 7 Bundesräte.

Dann gibt es die 7 Zwerge, 7 Samurai, 7 Weltwunder³, die 7 Todsünden⁴etc.

³ Die hängenden Gärten zu Babylon, Koloss von Rhodos, Grab des Königs Mausolos II. zu Halikarnassos, Leuchtturm auf der Insel Pharos vor Alexandria, Pyramiden von Gizeh in Ägypten, der Tempel der Artemis in Ephesos, die Zeusstatue des Phidias von Olympia

⁴ Hochmut, Geiz, Wolllust, Zorn, Völlerei, Neid, Faulheit. Interessanterweise stehen den 7 Todsünden 10 Gebote gegenüber.

Die 7 ist eine Primzahl.

Die Acht

8 Planeten in unserem Sonnensystem. 

Alle Sterne, die am Himmel selbständig leuchten sind Sonnen. Die Planeten, die wir auch am Himmel sehen, reflektieren das Licht unserer Sonne.

Das Oktalsystem wird eingesetzt, um die Progammierung zu vereinfachen.

Analog Beschrieb im Abschnitt „Oktave“, schreibt man die 8 als 10:

01  02  03  04  05 06 07  10

11  12  13  14  15 16 17  20

Die Neun

9 ist die höchste der Grundziffern (1 – 9).

Eine Randbemerkung zum Wort Ziffer: Man könnte sagen, die Ziffer entspricht dem Buchstaben und die Zahl dem Wort. So gesehen ist der Ausdruck Zifferblatt falsch, weil 11 und 12 Zahlen sind, die je aus 2 Ziffern bestehen.

Die Neun gilt als Zahl der Vollkommenheitd da sie dreimal die in vielen Kulturen als „göttlich“ angesehene Zahl 3 enthält.

 (Im Kontrast zu 666, Symbol des Satans) 

Es gibt den Film „Die neunschwänzige Katze“ (der nicht sehr gute Kritiken erhielt). Der Filmtitel enthält den Verweis auf eine neunschwänzige Peitsche (neunschwänzige Katze genannt), die zur Bestrafung in der Seefahrt verwendet wurde.

Die Fibonacci-Zahlen

Benannt ist diese Zahlenfolge nach Leonardo Fibonacci , der damit im Jahr 1202 das Wachstum einer Kaninchenpopulation beschrieb.

Die Folge war aber schon in der Antike, sowohl den Griechen als auch den Indern bekannt.

Die Fibonacci-Folge beruht auf einer Beziehung zwischen vorhergehender und nachfolgender Zahl, was auch auf Wachstumsprozesse in der Natur verweist:

Also: 1:2:3:5:8:13:21:34 …

Je weiter man in der Folge fortschreitet, desto mehr nähert sich das Verhältnis zweier benachbarter Zahlen dem Goldenen Schnitt (1,618033…)

Z.B 55:34 = 1,6176...

Der Goldene Schnitt

Grundsätzlich liegt dem Goldenen schnitt das selbe Prinzip zugrunde, wie das der Fibonacci-Folge: Das Verhältnis des Ganzen zu seinem größeren Teil entspricht dem Verhältnis des größeren zum kleineren Teil.

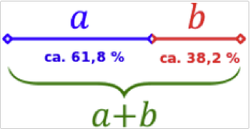
Der Goldene Schnitt war schon in der Antike bekannt. Allerdings wurde der Begriff Goldener Schnitt erst ab der ersten Hälfte des 19. Jahrhunderts gebraucht. Möglicherweise im Zusammenhang mit dem Klassizismus, der um diese Zeit Architektur und Kunst prägte und sich auf die antiken Werte besann.

Zitate aus Wikipedia zum Thema „Goldener Schnitt“:

Natur: Das spektakulärste Beispiel für Verhältnisse des Goldenen Schnittes in der Natur findet sich bei der Anordnung von Blättern (Phyllotaxis) und in Blütenständen mancher Pflanzen. Bei diesen Pflanzen teilt der Winkel zwischen zwei aufeinander folgenden Blättern den Vollkreis von 360° im Verhältnis des Goldenen Schnittes, wenn die beiden Blattansätze durch eine Parallelverschiebung eines der Blätter entlang der Pflanzenachse zur Deckung gebracht wird. Es handelt sich um denGoldenen Winkelvon etwa 137,5°.

Die daraus entstehenden Strukturen werden auch als selbstähnlich^A bezeichnet: Auf diese Weise findet sich ein Muster einer tieferen Strukturebene in höheren Ebenen wieder. Beispiele sind die Sonnenblume, Kohlarten, Kiefernnadeln an jungen Ästen, Zapfen, Agaven, viele Palmen- und Yuccaarten sowie die Blütenblätter der Rose, um nur einige zu nennen.

Architektur der Antike: Frühe Hinweise auf eine Verwendung des Goldenen Schnittes stammen aus der Architektur. Die Schriften des griechischen Geschichtsschreiber Herodot zur Cheops-Pyramide werden gelegentlich dahingehend ausgelegt, dass die Höhe der Seitenfläche zur Hälfte der Basiskante im Verhältnis des Goldenen Schnittes stünde. Die entsprechende Textstelle ist allerdings interpretierbar. Andererseits wird auch die These vertreten, dass das Verhältnis (Pi) für Pyramidenhöhe zu Basiskante die tatsächlichen Maße noch besser widerspiegele. Der Unterschied zwischen beiden vertretenen Thesen beträgt zwar lediglich 3,0 %, ein absoluter Beweis zugunsten der einen oder anderen These ist demzufolge damit aber nicht verbunden.

Viele Werke der griechischen Antike werden als Beispiele für die Verwendung des Goldenen Schnittes angesehen, wie die Vorderfront des 447–432 v. Chr. Unter Perikles erbauten Parthenon-Tempels auf der Athener Akropolis. Da zu diesen Werken keine Pläne überliefert sind, ist nicht bekannt, ob diese Proportionen bewusst oder intuitiv gewählt wurden. Auch in späteren Epochen sind mögliche Beispiele für den Goldenen Schnitt, wie der Dom von Florenz, Notre Dame in Paris oder die Torhalle in Lorsch 770 n. Chr. zu finden. Allerdings ist die bewusste Anwendung des Goldenen Schnittes anhand der historischen Quellen nicht nachweisbar.^B

^ASelbstähnlichkeit ist auch ein wichtiges Prinzip bei den Fraktalen von Benoît Mandelbrot (auch bekannt als Apfelmännchen).

^B Auch wenn wir den Goldenen Schnitt nicht kennen, kommen wir diesem intuitiv nahe, wenn wir harmonische Verhältnisse kreieren. In der Natur erscheint der Goldene Schnitt aus dem Wachstumsprozess heraus. Der Goldnen Schnitt hat die Qualität eines Naturgesetzes.

Anzahl Beine bei Tieren

2 Beine: Vögel. Um sich an die Ästen klammern zu können, haben die meisten Vögel 3 „Finger“⁵ und einen „Daumen“⁶.

4 Beine: Säugetiere, Reptilien und Amphibien. Ähnlich der Vögel haben Reptilien „Finger“, jedoch deren 5, in der Regel ohne „Daumen“. Amphibien haben 4 Finger an den Händen und 5 „Finger“ an den Füssen. Bei Säugetieren redet man von Vorder- und Hinterbeinen. Ausser bei Nagetieren, Primaten und Menschen, wo man von Armen und Beinen spricht. An den Händen haben diese 5 Finger, wobei die Nagetiere⁷ keinen Daumen⁶ haben. Dafür haben die Nagetiere und Primaten auch an den Füssen „Finger“⁵, während man beim Mensch von Zehen spricht. Die anderen Säugetiere haben Pfoten/Tatzen, Klauen und Hufe (deren Knochenstruktur auf fünf Gliedern basiert).

⁵„Finger“ stehen in Anführungszeichen, weil man normalerweise an den Füssen von Zehen spricht. Finger sind lang ausgebildet und haben die Fähigkeit zu greifen, im Gegensatz zu Zehen. Genau genommen hat nur der Mensch Zehen. Elefantenfüsse sind ähnlich, mit 4 Zehen (die 5. ist in der Knochenstruktur vorhanden, aber, wie bei den Tieren mit Pfoten, verkümmert)

⁶ Der Daumen ist jener Finger, der den anderen gegenüber liegt und das Greifen viel effizienter macht.

⁷In Bezug zu den Händen sind die Nager dem Menschen ähnlicher, als z.B. Katzen oder Hunde. Bei letzteren sind es die Sozialinstinkte die die Voraussetzung für emotionale Bindungen zwischen Mensch und Tier ermöglichen. Anderen Haustiere wie Meerschweinchen, Ratten und Vögel (z.B. Raben) nehmen zwar auch soziale Kontakte zu Menschen auf. Diese müssen aber in Käfigen gehalten werden, da man sie nicht zur Stubenreinheit erziehen kann.

6 Beine: Insekten. Interessant ist, dass die Vorstufe des Schmetterlings, die Raupe, 16 „Beine“ hat. Nachdem der Schmetterling aus der Puppe geschlüpft ist, hat er 6 Beine.

8 Beine: Spinnen

Anm. Insekten, Spinnen, Krebse und Tausendfüssler gehören zur Gruppe der Gliederfüsser. In dieser Gruppe gibt es Arten, die von 10 (Krebse) bis zu 800 Beine (Tausenfüssler) haben können.