Visuelle Konzepte     Tanz der Teiler D     Dance of the Dividers E

Zum Vergrössern anklicken

Der Tanz endet bei der Zahl, die durch alle Grundzahlen von 1 bis 9 teilbar ist.

Angefangen hat es damit, dass ich mir Gedanken zur Zahl 12 gemacht habe. Für mich hat diese Zahl etwas Bedeutungsvolles, aber auch Altmodisch--Mittelaterliches. 12 Zoll entsprechen einem Fuss, am Markt kauft man ein Dutzend Eier undsofort.

Dem Dutzend den Vorzug zu geben gegenüber der dezimalen Zehn, liegt vielleicht daran, so spekuliere ich, dass das Dutzend mehr Teiler enthält, als die Zehn. So kann man 12 durch 2, 3, 4 und 6 teilen, während 10 nur durch 2- und 5 teilbar ist, vorausgesetzt, wir bewegen uns in der Welt der natürlichen Zahlen..

Das grundsätzlichste Prinzip intellektuellen Denkens ist die Dualität, das Denken in Gegensatzpaaren, das wir in Wissenschaft, Philosophie und Religion wiederfinden. (z.B. Plus-/Minus, Gut und Böse, Ein/Aus, Endlich/Unendlich.) Das Endliche ist einfach zu erkennen – als Gegensatz schliessen wir auf das Unendliche, dass sich unserer Vorstellungskraft entzieht. Viele Entscheidungsprozesse beginnen mit ja oder nein. Im Yin-Yang-Symbol ist die Dualität dargestellt. Das Prinzip von These und Antithese, von denen jede einen Kern ihres Gegenteils in sich trägt.  Aus These und Antithese lässt sich die Synthese ableiten. Das bringt uns zur Zahl 3. Für die Drei gibt es etliche mythische Referenzen. Z.B. „Vater, Sohn und heiliger Geist“ (die heilige Dreifaltigkeit).

Die Verdoppelung von 2 und 3 ergibt 4 und 6. Darauf ist z.B. das I Ging (chinesisches Orakel) aufgebaut. 1 (ungerade) ergibt eine durchgehende Linie, 2 (gerade) ergibt eine unterbrochene Linie. Ein fertiges Symbol besteht aus 2 Gruppen von 3 übereinander liegenden Linien (= 6 Linien), auch Hexagramm genannt.

Diese Logik, die auf 2 und 3 aufbaut führt uns auch wieder zur Zahl 12.

Davon ausgehend, dass der Vorteil des Dutzends in seiner hohen Teilbarkeit liegt, fragte ich mich, welches wohl die erste Zahl ist, die durch alle Grundzahlen von 1 bis 9 teilbar ist. Diese Zahl kann man als das Gegenteil einer Primzahl betrachten (die keine Teiler enthält ausser, was unvermeidlich ist, 1 und sich selbst). 

Das wäre dann die Suche nach der «Anti-Primzahl». 

Oder die Suche nach dem kgV, dem kleinsten gemeinsamen Vielfachen von 1 bis 9. Das kann man mit der Primfaktoren-Zerlegung ausrechnen und schreibt sich wie folgt: kgV (1,2,3,4,5,6,7,8,9) = ?

Ich hatte aber Lust, die Lösung dieses Problems ohne Formeln, unter Zuhilfenahme eines visuellen Systems, anzugehen.

So habe ich mir folgendes Experiment ausgedacht:

Ein Diagramm, auf dessen senkrechter Achse (y) die Teiler 1 bis 10 stehen und auf der waagrechten Achse (x) die Zahlen von 1 bis zu jener die schliesslich durch alle Grundziffern teilbar ist. 

Wenn die gesuchte Zahl durch alle Grundziffern teilbar sein soll, also die Teiler 2 und 5 zwingend vorkommen, weiss ich, dass die gesuchte Zahl durch 10 teilbar sein muss. Es genügt deshalb, die Zahlen in 10-er Schritten einzusetzen. 

Das nicht-mathematische Vorgehen:

Grundsätzlich brauche ich 10 Grundelemente, deren jedes einen Teiler repräsentiert. Also für die 1 ein Teil von 1x1 Einheiten, für die 2 eines von 2x1 Einheiten, für die 3 dementsprechend 3x1 Einheiten undsofort. Wenn ich genügend dieser Teile logisch anordne, komme ich irgendwann zu einer Säule, auf der alle Teiler vorkommen. Ich weiss inzwischen, dass dies bei 2520 der Fall ist.

Ich weiss auch, da ich nur die Zahlen der Zehnerreihe einsetze, dass Zeilen der 1er, 2er, 5er und 10er-Teiler durchgehende Balken ergeben. Was ich beim Experimentieren auch schon entdeckt habe, ist, dass sich das Muster (in der 10-Teiler-Konfiguration) nach 36 Kolumnen wiederholt – ausser bei der Zahl 7*. Das eröffnet grundsätzlich neue Möglichkeiten, die grafische Umsetzung anzugehen.

--> Siehe Grafik "7er-Wanderung"

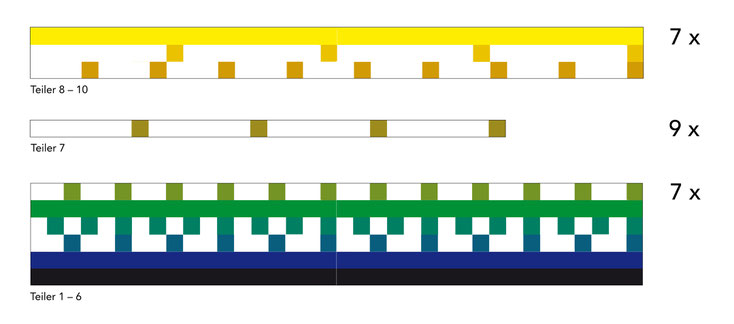
Ich möchte aber vorerst beim Vorgehen mit Teilstücken verweilen. Um auf handwerklichem Weg zu einer Darstellung zu kommen, kann ich anstelle der Säulen, die die einzelnen Zahlen darstellen, Streifen kreieren, die jeweils einen bestimmten Teiler repräsentieren. 

Beginnen wir ganz lakonisch bei Teiler 1. Alle Zahlen sind durch 1 teilbar. Also entsteht hier ein durchgehender Balken. Das gilt auch für Teiler 2, sowie 5 und 10, weil wir in unserem Experiment nur die Zahlen der Zehner-Reihe benutzen.

Für den Teiler 3 kann ich Streifen herstellen, auf denen jede 3. Position eingefärbt ist. Analog ist beim Teiler 4 jede 2. Position eingefärbt. In der selben Weise gehen wir für die Teiler 6 und 8 vor, bei denen jede 3. bzw. 4 Position eingefärbt ist. Bei der 7 ind 9 sind nur die 7. und 9. Position eingefärbt

*Es ergeben sich 7 36er-Pakete. Ohne die 7er-Reihe, die sich als einzige gegenüber den anderen verschiebt, wäre der Tanz schon bei 360 zu Ende. 

Das sieht so aus: